Search Algorithms

Linear Search

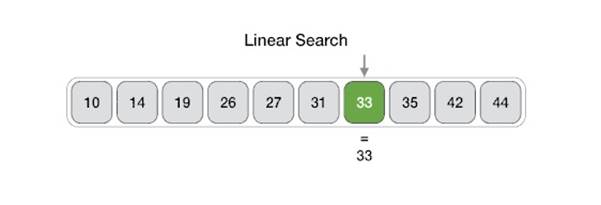
Linear search, also known as sequential search, is a simple search algorithm that checks each element in a list one by one, starting from the beginning, until the target element is found or the end of the list is reached. It is suitable for unsorted or small-sized lists. Linear search has a time complexity of O(n), where n is the number of elements in the list.

Binary Search

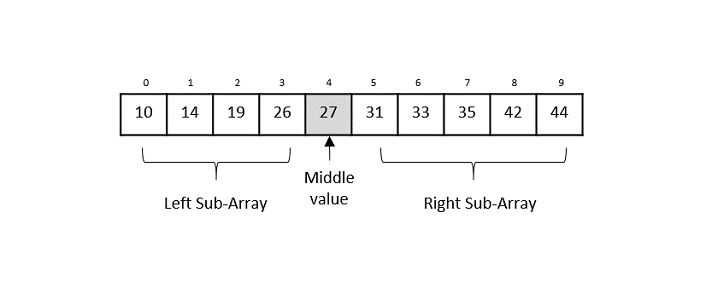
Binary search is a more efficient search algorithm that works on sorted lists. It repeatedly divides the list in half and compares the middle element to the target element. Based on the comparison, it discards the half of the list that does not contain the target and continues the search in the remaining half. It reduces the search space significantly with each step. Binary search has a time complexity of O(log n), where n is the number of elements in the list. This makes it much faster than linear search for large lists.

Exponential Search

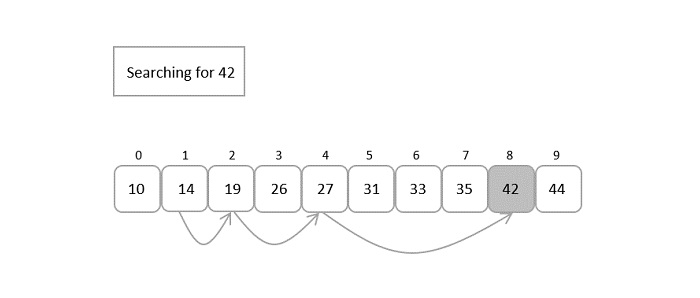
Exponential search is an improvement over linear search for large, unbounded lists. It involves two steps: first, it searches for a range where the target element might exist by repeatedly doubling the index until a value larger than the target is found. Then, it performs a binary search within that range to find the exact target element. Exponential search has a time complexity of O(log i), where i is the index of the found range. This makes it faster than linear search, especially for large lists.

Jump Search

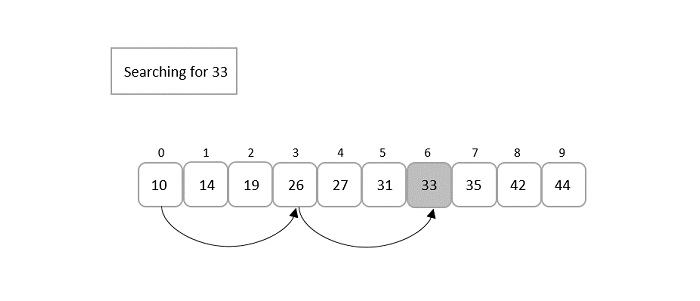
Jump search is another search algorithm for sorted lists. It divides the list into fixed-size blocks and performs a linear search within each block. If the target element is found in a block, the search is successful. Otherwise, it moves to the next block and repeats the process until the target element is found or the end of the list is reached. Jump search has a time complexity of O(√n), where n is the number of elements in the list. It is faster than linear search but generally slower than binary search on large lists.